Números Imaginarios

Raíz imaginaria de la unidad negativa

¿Qué es un número imaginario?

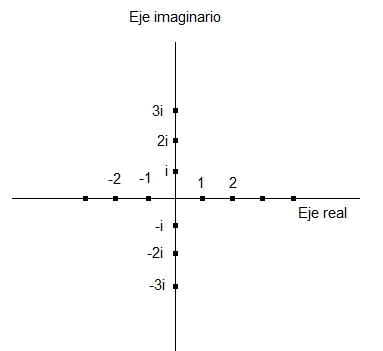
Un número imaginario es cuando la raíz cuadrada del número real está multiplicada por el factor raíz cuadrada de menos uno, que realmente se representa con la letra i como se muestra en la primera imagen.

Ejemplos: 

Potencia de los números imaginarios

Como ya sabemos, la raíz cuadrada es la operación inversa al exponente cuadrado, entonces, sabiendo que un número multiplicado por sí mismo equivale a elevarlo al cuadrado, podemos expresar esto como:

El conjunto de los números Complejos

El conjunto numérico que contiene todos los números se denomina conjunto de los números complejos. 

Los números complejos son una extensión de los números reales y forman el mínimo cuerpo algebraicamente cerrado.​ El conjunto de los números complejos se designa con la notación ${\displaystyle \scriptstyle \mathbb {C} }$, siendo ${\displaystyle \scriptstyle \mathbb {R} }$ el conjunto de los números reales se cumple que ${\displaystyle \scriptstyle \mathbb {R} \subset \mathbb {C} }$ (${\displaystyle \scriptstyle \mathbb {R} }$ está estrictamente contenido en ${\displaystyle \scriptstyle \mathbb {C} }$). Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. 

Un número complejo es un número formado por una parte real y una parte compleja como se muestra en la siguiente imagen.

Representación gráfica 

Para representar gráficamente un número complejo, debemos dibujarlos en el plano complejo. Éste está formado por un eje real y un eje imaginario. Sobre el eje real representaremos la parte real del número complejo, mientras que en el eje imaginario representaremos la parte imaginaria. Dichos ejes los dibujaremos perpendiculares y secantes en el cero, que tiene parte real e imaginaria nula.

Si queremos representar un A= a+bi  se dibuja en el plano el vector asociado a "A" que es el vector con origen (0.0) y extremo el punto (a, b). 

Ejemplo: 

https://www.sangakoo.com/es/temas/representacion-de-numeros-complejos-en-el-plano 

Suma y resta de números complejos

Analiza los siguientes resultados: Para sumar 3a+7b con 6a+8b se hace de la siguiente manera:

(3a+7b) + (6a+8b) = (3a+6a) + (7b+8b) = 9a+15b

Ahora si quieres sumar 3a+7b con 6a+8b procederías de la misma forma que la anterior y nos quedaría así:

(3a+7i) + (6a+8i) = (3a+6a) + (7i+8i) = 9a+15i

Por otro lado, si se trata de restar 5a+3b de 3a+2b, tendríamos:

-(5a+3b) + (3a+2b) = (-5a + 3a) + (-3b+2b) = -2a-b

Ahora si procede de la misma manera y resta 5a+3i de 3a+2i, así:

-(5a+3i) + (3a+2i) = (-5a + 3a) + (-3i+2i) = -2a-i

Observa que la suma y la resta de números complejos obedece a las mismas reglas para sumar y restar algebraicamente dos polinomios,

Ejemplos:

1.     Sumar 6-3i con -2+4i

Solución: 6-3i + (-2+4i) = (6-2) + (-3i+4i) = 4+i

2.     Si de -7+4i se resta 3-8i

Solución: -7+4i - (3-8i) = (-7-3) + (4i+8i) = -10+12i

https://www.montereyinstitute.org/courses/DevelopmentalMath/TEXTGROUP-15-19_RESOURCE/U16_L4_T2_text_final_es.html 

Guía de curso